Problem of the Day

Problem:

A Fibonacci sequence that starts with 0 (the 0th element), and 1 (the 1st element), continues on from there, with subsequent values in the sequence being calculated as the sum of the two previous values.

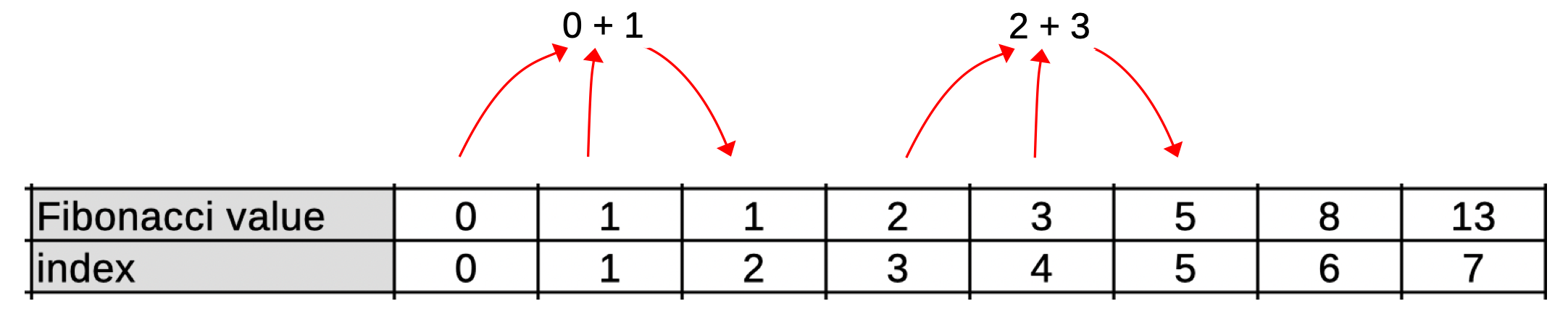
Given the recursive method fib shown here, which calculates and returns the nth value in the Fibonacci sequence, how many times would fib be called in calculating the 4th Fibonacci number?

public static int fib(int n)
{
    if (n == 0 || n == 1)
        return n;
    else
        return fib(n - 2) + fib(n - 1);
}

2 times
3 times
9 times
15 times
25 times

Show solution:

The correct answer is c. The function is called once for the number 4, which requires calls for 3 and 2, which in turn requires calls for 2 and 1 (for 3), as well as 1 and 0 (for 2). The call for 2 requires two additional repeated calls for 0 and 1, making a total of 9 function calls. Calculating Fibonacci values by simple recursion is not a very efficient process!