Problem of the Day
Friday, March 13, 2026
Problem:
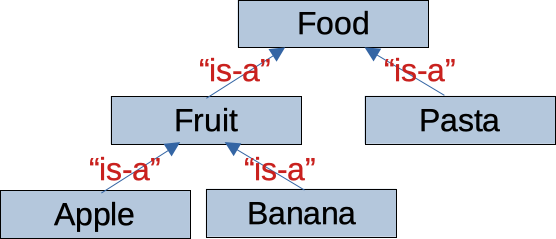
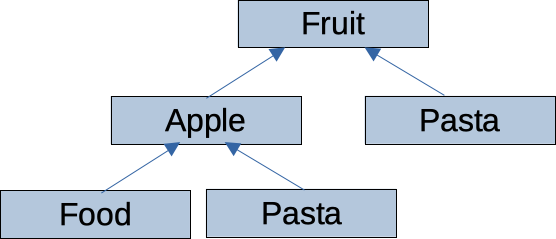
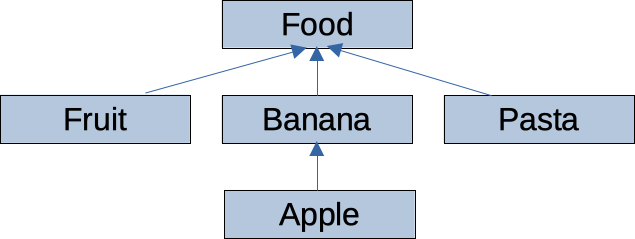
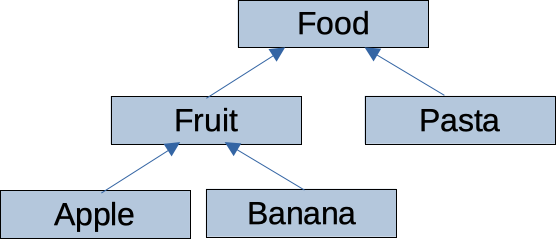
A series of classes manage a variety of items that can be eaten: Fruit, Food, Banana, Pasta, and Apple. Which diagram represents the superclass-subclass relationships between these classes?
The correct answer is d. The arrows in the class diagram indicate the "is-a" relationships between the superclasses and subclasses: Fruit and Pasta both inherit from ("extend") Food, and Apple and Banana inherit from Fruit.